Czy trójkąt może mieć dwa kąty proste, a 0,(9) być równe 1?

O tym, jak nieskończoność uwodzi intuicję - ale nie łamie matematyki.

Wstęp

Granica. Nieskończoność. Asymptota. Słowa, które brzmią abstrakcyjnie, ale mają bardzo konkretne konsekwencje. Istnieją zjawiska, które na pierwszy rzut oka wydają się sprzeczne z intuicją - jak trójkąt z dwoma kątami prostymi albo równość 0,(9) = 1. Ale to nie błędy. To granice^[1].

Trójkąt z dwoma kątami prostymi?

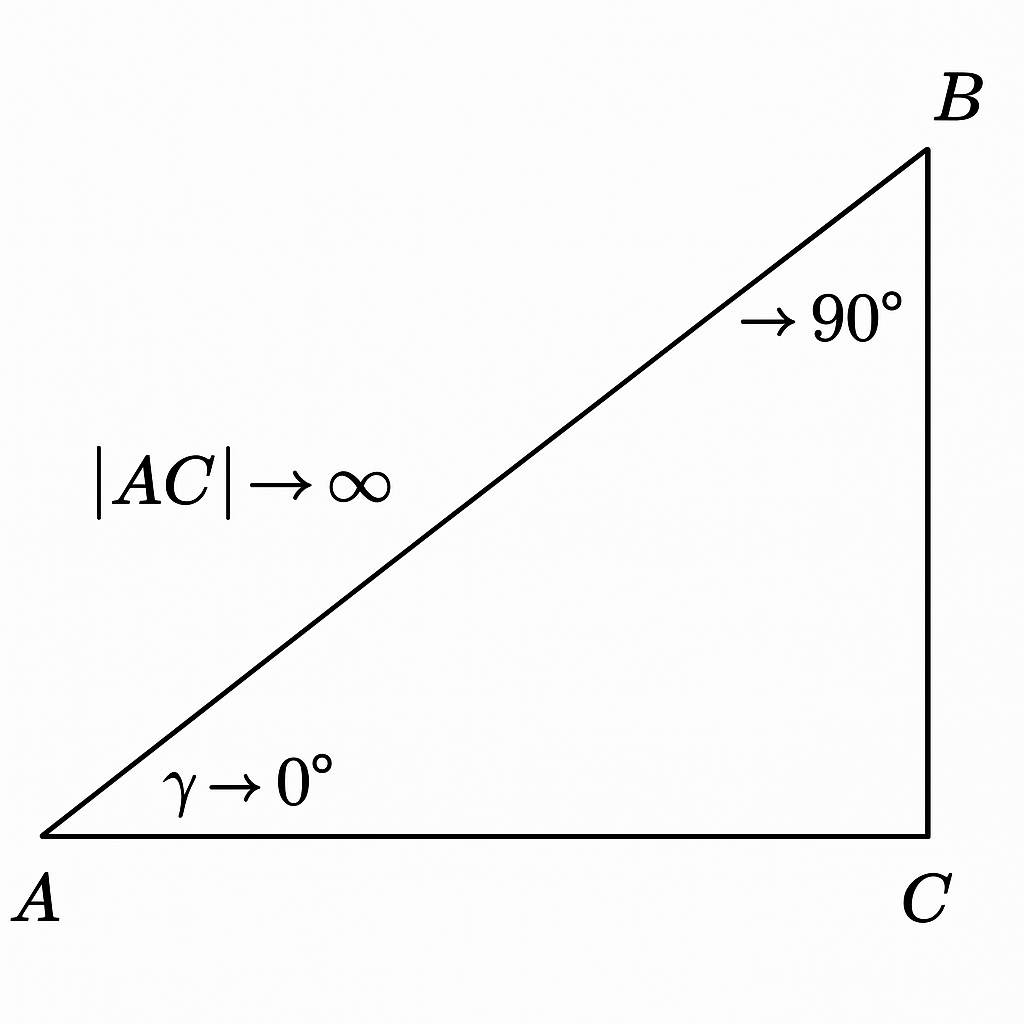
Rozważmy trójkąt prostokątny ABC, w którym kąt przy wierzchołku C to dokładnie 90°, a jedno z ramion, powiedzmy |AC|, dąży do nieskończoności. Co się dzieje z resztą trójkąta?

• Kąt przy wierzchołku B asymptotycznie zbliża się do 90°.
• Kąt przy A maleje do 0°.
• Przeciwprostokątna AB staje się równoległa do ramienia AC.

W granicy otrzymujemy układ, który wygląda jak trójkąt z dwoma kątami prostymi - pozorna sprzeczność. Ale granica nie jest tym samym co „osiągnięta wartość”^[2]. W każdej konkretnej konfiguracji kąt B jest mniej niż 90°, a A większy niż 0°. Suma zawsze daje 180°.

0,(9) = 1 - czyli nieskończony ogonek

Drugim przykładem z tej samej klasy jest równość:

1 ÷ 3 = 0,(3)  
0,(3) × 3 = 0,(9) = 1

To nie przybliżenie. To ścisła równość w granicy. Liczba 0,(9) to nieskończony ciąg dziewiątek. Każda jego skończona wersja - 0.9, 0.99, 0.999 , jest mniejsza od 1, ale ciąg tych przybliżeń zbiega do 1^[3].

W granicy:
lim (n → ∞) [1 - 1/10ⁿ] = 1

Więc 0,(9) = 1  mimo że „na oko” wydaje się trochę mniejsze.

Co je łączy?

• Oba przykłady to granice ciągów.
• Oba pokazują pozorną sprzeczność, która znika przy ścisłym rozumieniu granic.
• W obu nieskończoność nie jest liczbą, lecz procesem - nigdy nie osiąganym, zawsze przekraczanym.
• I w obu przypadkach matematyka pozostaje wewnętrznie spójna^[4].

Na zakończenie: asymptota nie jest końcem

W projekcie „Wektor Ciekawości” takie zjawiska będą się pojawiać wielokrotnie: w granicach trajektorii, w oscylacjach sinusoidalnych, w strukturach przestrzeni. Granica to narzędzie - nie pułapka. Ale wymaga ostrożności i dyscypliny myślenia.

Jeśli coś wydaje się paradoksalne - być może dotarliśmy właśnie do asymptoty intuicji. A za nią zaczyna się matematyka.

1. [1] Granice są fundamentem rachunku różniczkowego i całkowego. Zostały formalnie zdefiniowane w XIX w. przez Cauchy’ego i Weierstrassa.
2. [2] Granica ciągu to wartość, do której dąży ciąg, ale nie musi jej osiągać w żadnym skończonym kroku.
3. [3] Dowód: Niech x = 0,(9). Wtedy 10x = 9,(9). Odejmując: 10x - x = 9 ⇒ x = 1.
4. [4] Oba przypadki są spójne z aksjomatami analizy matematycznej, nawet jeśli kolidują z intuicją bazującą na liczeniu pieniędzy lub mierzeniu desek.